Home A - Z
Page Index

Investing with leverage

General investing advice and information with a focus towards using leverage.

Basics

I recommend the Bogleheads theory of investing. This involves investing in a few ETFs or mutual funds as a diversified portfolio. For example, a 3 fund portfolio. I use Schwab funds, but any with low expense ratios will suffice. This is a set and forget strategy that requires very little work.

An important piece is figuring out your asset allocation for each fund. The simplest setup is just use a target date fund, picking your expected retirement year. SWYGX is one such Schwab fund with a target retirement date of 2040.

TDFs follow a glide path that generally invests in stocks when you are young (higher risk), and moves towards bonds as you get older (less risk). You can push the target year later than your normal retirement year if you are comfortable with more risk for a longer time.

Target date funds are not a good idea for a taxable brokerage account. They are mainly only good for a 401k or IRA accounts for tax reasons. See this thread and this SEC filing for why.

This brings up an important question: are there TDF-like funds that can be used in a taxable account? Yes, iShares has some. This reddit thread has some good pointers.

The book The Simple Path to Wealth is great and describes an even simpler way by just investing in one total market fund (VTSAX). In most cases this is all people need to do basic investing with reasonable return.

Diversifying further

Though the above combination of stocks and bonds is perfectly reasonable, I like to diversify further into a few other categories. Mainly I add the following, either in ETFs, futures, or physical assets where applicable:

Category ETFs Futures Physical
Gold GLD, GLDM, SGOL /GC, /MGC Bullionstar
Silver SIVR /SIN Bullionstar
Cryptocurrency IBIT, MSTR /MBT Ledger

These in sum do not exceed about 8% of my portfolio. I reduce my bonds allocation by 8% to make room for these. The reasoning is to keep some investments non-correlated with stocks/bonds.

Schwab ETFs do not have much option liquidity. For such cases, I might use different ETFs or futures to represent the same category. Sometimes it is also cheaper to purchase ETFs with a higher price due to trading fees being based on number of shares. I also may use mutual funds if I don't plan to do much active trading. Some equivalents:

Category ETFs/funds Futures
US Total Market SCHB, VTI, SWTSX, VTSAX
US Large Cap SCHX, SPYM, SPY, VOO, VV /MES, /ES
US Small Cap SCHA, VB, IWM /M2K, /RTY
US Bonds BND, SCHO, SCHR, SCHZ, SWAGX, TLH, TLT /MTN, /10Y (inversely correlated)
International Developed SCHF, SWISX, EFA, VEA /MFS (MXEA)
International Emerging SCHE, EEM, VWO /MME (MXEF)

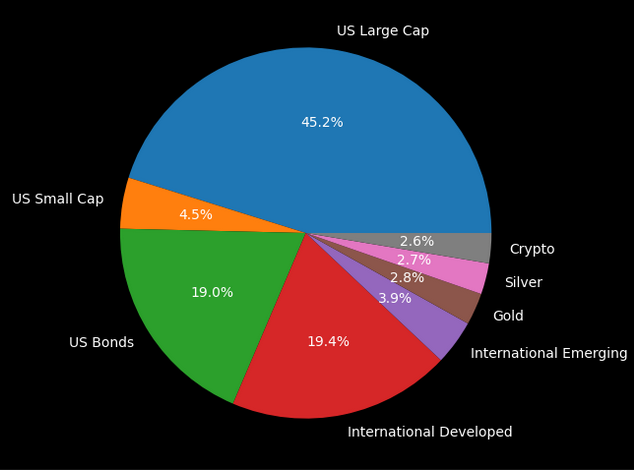
Here is an example of my allocation as of June 2025:

Holding cash

Banks and brokerages give little in return for holding your cash. A HYSA will give you better return, but sometimes suffer from bad checking account features. For example, Wealthfront has very bad check-writing abilities.

Excess cash in your brokerage should be put into a money market fund. For example, at Schwab you can use SWVXX. The key point is many brokerages won't automatically sweep to this for you, so it requires you to do trades. SGOV and BIL are other good ETFs for this. You can find good money market funds at Yieldfinder.

If you don't do this yourself, your brokerage will love your idle cash sitting around which they will use to invest and earn them, and not you, money. I do not hold much cash because inflation quickly eats into its value. I'd rather put that money to better use.

Rebalancing

Occasional portfolio rebalancing is necessary unless you are only invested in an automatic glide path fund. I just contribute funds to the deficient allocation category. If it requires a much higher amount than the funds available, utilizing leverage can get me to a balanced portfolio quicker.

The paper Rebalance your portfolio without selling describes some more ways to optimize rebalancing.

By utilizing derivatives when rebalancing, I can turn a buy into a sell and vice versa. The notional values of long or short derivatives can simulate a reduction or an increase in that asset class. As an example, let's say I need to sell $4000 of large cap to rebalance. Instead of selling that stock, I can buy a put, which will have a negative notional value. Say SPYM is trading at 80. A .50 delta PUT 200 days out might cost $400. By buying that, I've created a negative notional value that can be added to my large cap balance:

\[\text{Notional Value} = 80 \times 100 \times .50 \times -1 = -4000\]

If I needed to sell $8000, I could by 2 of these. What if I wanted to spend less? I could create a synthetic short: sell a call, and buy a put (essentially funding it with the sold call), at strike price 80. For larger sums, I might use SPY or futures.

As another example, let's say I need to buy $4000 of large cap to rebalance. Instead of buying that stock, I can sell a put, which will have a positive notional value. Similar to above:

\[\text{Notional Value} = 80 \times 100 \times .50 = 4000\]

Instead of spending money on a buy, I am actually receiving money by selling the put. Once you understand derivatives as building blocks, you can convert transactions to/from buy/sell easily.

Efficient use of capital

One of the most important things I've come to realize is that you have to make efficient use of your capital. Tom Sosnoff and Tastytrade have some good videos on this:

The main question to ask yourself is are you using your capital the best way possible? In many cases your brokerage is giving you access to tools and methods to make better use of that capital. They will not tell you all of these methods, which one is best, or hold your hand through the process, unless you pay them.

Capital efficiency example

Let's say you wanted to invest in the S&P 500 in a buy and hold fashion. The following are some examples and costs associated:

Instrument Cost Exposure Leverage
50 shares SPY @ $590 $30k $30k 1x
50 shares SPY @ $590 + 25 shares with margin loan $30k + interest $45k 1.5x
1 90-delta DITM LEAPS SPY call $20k $40k 2x
1 synthetic LEAPS in SPY (long call, short put) $2k $60k 30x
1 ZEBRA LEAPS in SPY (2 long calls, 1 short call) $14k $50k 3.5x
1 /MES future $2k $30k 15x

In all cases but the first, you are paying less to have a higher exposure in the same market. Each has a different risk profile, generally increasing with leverage. In all cases you can lose money.

Only the first two cases involve actually owning shares. For derivatives, it is not too important whether you end up with shares or not, as the P/L will be similar to owning the exposed amount. They also have expirations, but you can continually roll them to future dates to simulate a buy and hold.

General investing goal

I take the idea of having an diversified portfolio and just add leverage to it. In other words, I keep the same desired percentages of each category, and use the notional value of derivatives to represent to amount invested in that category. The diversified portfolio I follow is a target date fund, such as SWYGX. As these percentages change over time, I do rebalancing taking into account the leverage I'm using.

This method of using leverage is also referred to as "return stacking", and there are some ETFs that also try to do this for you.

Leverage

Adding leverage increases your risk, but increased risk is one way to possibly gain better returns. There are many ways to gain leverage, from using loans, to options, to futures.

A fundamental question is how much leverage you want to use. Brokerages make it all too easy to over-leverage. I usually use a leverage ratio between 1.5 - 2.5. For example, if I have $100k cash, I may use that to invest a notional value of $150k in a diversified portfolio. A typical hedge fund might use a leverage ratio up to 5, so this is not exceedingly risky.

People use leverage all of the time for home loans, and it is not unheard of to use a 80% loan to value ratio for a mortgage, or a leverage ratio of 5. For a $500k home, you might put up $100k cash and take a $400k loan. You would likely do this at a reasonable interest rate, and your hope is the value of the home goes up faster than your interest charges. Your home value could fall, leaving you with a mortgage that is underwater, i.e. you owe more than the home is actually worth. You could also lose your home in a disaster. All of this can apply to investing as well.

A typical company might use a loan to ultimately produce something worth more than that loan, in a sense making a leveraged bet. You could argue companies would not exist without such leverage. Even credit card debt can be considered a form of very expensive leverage. If you acknowledge leveraging exists throughout the economy, then why not use it to your advantage in your personal finances as well?

The following book provides a good argument for using leverage. The general idea is use high leverage when young and reduce that leverage towards retirement:

This paper on risk parity generally describes how I use leverage.

Other forum threads:

Targets

When investing the extra cash that comes from leverage, it should be towards your desired asset allocation. That allocation should be a diversified portfolio (e.g. the Bogleheads portfolio). For example, if your current allocation is deficient in US large cap, you can use the cash from leverage to increase that particular allocation.

Definition

We'll use the following for the definition of leverage ratio:

\[\text{Leverage Ratio} = \frac{\text{Notional Exposure}}{\text{Portfolio Equity}}\]

Notional Exposure includes:

  • Total value of all equities
  • Options notional exposure
  • Futures notional exposure

Portfolio Equity includes:

  • Total value of all equities
  • Options value
  • Cash
  • Margin balance (negative)
  • Futures required good faith deposit (negative)
  • Futures profit (positive) or loss (negative)

Suppose I have $130k in equities. I borrowed $30k as a margin loan for that position. My leverage ratio comes out to:

\[\text{Leverage Ratio} = \frac{130000}{130000 - 30000} = 1.3\]

Notional exposure vs value

Options

The numerator of the leverage ratio should include the notional exposure of options. There are different ways of calculating this. A simple way is to use the delta notional exposure (also referred to as delta dollars):

\[\text{Delta Notional Exposure} = \text{Delta} \times \text{Strike} \times \text{Contracts} \times \text{Multiplier}\]

The denominator should include only the market value of the option contract itself.

Futures

The numerator of the leverage ratio should include the notional exposure of futures. This is different depending on the contract type. For indexes it is usually:

\[\text{Future Notional Exposure} = \text{Index Price} \times \text{Multiplier}\]

Futures do not cost anything, however I include the good faith deposit required in the denominator, as well as any gain or loss of the futures position.

Margin loan

When you have stocks, brokers will let you take a margin loan of at least 50% or more of your equity value. This gives you at least 1.5 leverage, at the cost of margin loan interest, which is usually terrible at most brokerages. For example, Schwab will charge you 13% interest as of today (June 2025). If you cannot make more than 13% on the investments you do with leverage, you won't even break even. Interactive Brokers will give you a much better rate, for example 5%. This is an easier number to beat on investment return.

This type of leverage is the simplest to use and understand. The broker will let you buy stocks without cash, making your cash balance negative, and charging daily interest on it. You can pay it back whenever you want, and your broker will prefer you pay it back later so they can keep charging you interest.

Forex margin loan

One way to reduce interest charges is using a forex margin loan (sometimes called a carry trade). Your broker may have a much lower interest rate for borrowing in another currency like CHF. Say that is 1.5%. You can take a CHF loan, convert that to USD, and use the funds to invest in US stocks. However, you must now beat both the 1.5% margin interest as well as any forex rate changes. For stable currencies like CHF, I've had good results for multi-year timeframes. However, if there is a big drop in USD value to the foreign currency, your loan repayment can be much bigger than you expected. Many people have done this with JPY due to its low interest rate.

You can use forex futures to lock in an interest rate for the loan. For example, buying a /6S future will offset any currency fluctuation with CHF.

Box spreads

A short box spread is another way to take a loan, except it is not from your broker, but from the options market. It is a combination of a synthetic long and synthetic short. This essentially gives you the best borrowing rate that your broker will never beat. This blog post describes the process. I created this video and slides going into the mechanics. Here is another good video about how this works.

Boxtrades is a good site for figuring out the trade to enter. You can even combine this with a forex carry trade to take the loan in another currency with lower interest rate, but you will need to be able to trade options in non-US markets (e.g. SMI index for CHF).

There are some fintech companies such as SyntheticFi offering to do these loans for you.

Derivatives

Options and futures can be used for their inherent leverage. There are many strategies to trade these, however this only focuses on their use as leverage.

Forum threads:

Options

One option contract represents 100 shares, and its cost is much less than actual shares. That should give you an idea of its leverage. In most cases you would only be trading the option and not be assigned shares. However, the profit/loss would be similar to as if you were actually trading 100 shares.

Buying DITM LEAPS Calls

This simply involves buying a long dated high delta call option. The high delta means it will most likely expire in the money, and will follow the actual stock price closely.

Overview video:

Example

Assume I have $100k invested in plain equities. I want to leverage up to 1.5 to invest in US large cap. I buy DITM LEAPS calls 1 year out in SPYM (a lower cost version of SPY), using the strike price for .90 delta:

  • 6 SPYM 2026-03-20 53 CALL

The exposure is:

\[\text{Delta Notional Exposure} = 0.90 \times 53 \times 6 \times 100 = 28620\]

The actual cost of the options might be $12700 in cash. That means $12700 is giving a notional exposure of $28620 in the S&P 500.

This gives an overall leverage ratio of:

\[\frac{(100000 + 28620)}{(100000 - 12700)} = \frac{128620}{87300} = 1.47\]
Synthetic long stock

This involves buying an ATM call and selling a put at the same strike. It is similar to using futures for leverage.

Overview video:

Example

Assume I have $100k invested in plain equities. I want to leverage up to 1.3 to invest in US large cap. I setup an ATM synthetic long 1 year out in SPYM:

  • 4 SPYM 2026-03-20 71 Call
  • -4 SPYM 2026-03-20 71 Put

Since they are ATM the delta will be .50 for both. The exposure is:

\[\text{Delta Notional Exposure} = (0.50 \times 71 \times 4 \times 100) + (-0.50 \times 71 \times -4 \times 100) = (14200) + (14200) = 28400\]

The actual cost of the position might be $500 in cash. That means $500 is giving a notional exposure of $28400 in the S&P 500. With portfolio margin, my buying power might be reduced by $3k to hold this position.

This gives an overall leverage ratio of:

\[\frac{(100000 + 28400)}{(100000 - 500)} = \frac{128400}{99500} = 1.29\]
ZEBRA

This involves buying 2 .70 delta calls, and selling a .50 delta call. These deltas can be adjusted a bit, but the general idea is it should total .90 delta or higher. It is similar to a synthetic long stock.

Overview videos:

Example

Assume I have $100k invested in plain equities. I want to leverage up to 1.7 to invest in US large cap. I setup a ZEBRA 1 year out in SPY:

  • 2 SPY 2026-06-18 545 Call
  • -1 SPY 2026-06-18 620 Call

The exposure is:

\[\text{Delta Notional Exposure} = (0.70 \times 545 \times 2 \times 100) + (0.50 \times 620 \times -1 \times 100) = (76300) + (-31000) = 45300\]

The actual cost of the position might be $14k. That means $14000 is giving a notional exposure of $45300 in the S&P 500. With portfolio margin, my buying power might be reduced by $6000 to hold this position.

This gives an overall leverage ratio of:

\[\frac{(100000 + 45300)}{(100000 - 14000)} = \frac{145300}{86000} = 1.69\]

Futures

A long futures contract on an equities index should behave similarly to owning an ETF, except that you have leverage.

Example

Assume I have $100k invested in plain equities. I want to leverage up to 1.3 to invest in US large cap.

1 /MES futures contract has a notional value of 5 * index price. Currently that is $30k. To long this contract, I am required to set aside $2500 as a good faith deposit for the contract. Note that the cost is essentially zero, except for commissions.

This gives me a notional exposure of $30k in the S&P 500 with a deposit of $2500. The $2500 is only the bare minimum, and it is usually advised to keep 2-5x of cash to handle downswings (see Futures vs equities margin).

This gives an overall leverage ratio of:

\[\frac{(100000 + 30000)}{(100000 - 2500)} = \frac{130000}{97500} = 1.33\]

General information

Bonds

I tend to look at bonds solely as a volatility hedge. I consider cash, usually in an account earning interest, and non-US retirement accounts in a different currency, such as a Swiss Pillar 2, as part of my bonds allocation.

There are some arguments to treat social security as part of your bonds allocation. It is more just an income source during retirement, and a bit difficult to calculate as a bonds value. I just don't consider social security at all in my investments or net worth.

Options

Videos

  • OptionStrat - Good tool for seeing P/L of various strategies

Futures

Futures vs equities margin

Futures margin is confusingly not the same as equities margin. When you buy or sell a futures contract, it costs nothing other than the commission. Instead, you put up in cash a good faith deposit. which is called its margin requirement. Every day, depending on whether the position moves for or against you, it is marked to market and funds are either deducted or added to your deposit. You get that deposit back, along with any profit or loss, when the contract closes.

Importantly, a futures contract requires actual cash. This is same for buying or selling a contract. The broker will let you borrow that cash from your equities account via a margin loan. This is different from an options trade which might only use your buying power and not require any cash or loan at all.

The main point is you need to have cash in your account to cover the margin requirement plus any possible losses in the futures contract. Typically people hold 2 to 3 times the margin requirement in cash just to be on the safe side.

Explanation from a Schwab rep:

I see you have been trading /MES so let's say you buy 1 /MES. First you will need to put up the house requirement needed to enter into the trade which will come out of your option BP (buying power), for /MES this is currently 2,550 per contract.

If you hold onto the /MES position through the futures market close, then there will be two different sweeps. The first is M2M (mark to market). M2M accounts for profits and losses during that day using the futures settlement price. Initially M2M will compare your trade price to the futures settlement price. If a profit is made, then we will move the excess profit from the futures cash balance to your cash & sweep vehicle. If it's a loss, then we will take cash from your cash & sweep vehicle and sweep it to the futures cash. If you were to hold /MES through more than one day, then it will compare today's settlement vs yesterday's settlement price.

The second cash sweep that will happen actually happens overnight. You will see this listed as "Cash Sweep" in ThinkorSwim. This overnight sweep is used to get the futures cash balance high enough to cover the exchange's initial requirement which is posted by the CME. As of today, for /MES the exchange initial requirement is 2,412.3 per contract for longs, however this does change every day. The overnight sweep moves the cash, so the futures cash balance equals the exchange initial requirement.

Explanation from Interactive Brokers:

The settled cash in both segments are summed when computing principal subject to interest, and the margin requirements for the futures are then backed out.

Principal is per currency and = total settled cash - short stock collateral - futures margin

Forum threads:

Futures instead of stock

Futures let you buy (or sell) into indexes like the S&P 500 and Russell 2000. A long /ES or /MES futures position should be equivalent to holding SPY shares. It is essentially an ETF without fees, however the longer-dated future price will be higher than the current index. There is an inherent loan when you long a future and interest is baked in.

For example, US small cap can be replaced with /RTY or /M2K. If my rebalancing requires I put $10k into US small cap, instead of buying the SCHA ETF, I might instead buy 1 /M2K future, which is currently the same notional value, but costs much less.

Forum threads:

Representing bonds with futures

The /10Y futures represents the current 10-year treasury yield. If the current yield is rising, it means newer bonds are worth more than older bonds. i.e. the return on newly issued bonds are greater than older issued bonds. The inverse should also be true.

ETFs like BND contain a mix of different types of bonds, but should be mostly older issued bonds. So what we should see is an inverse correlation of the /10Y future with the BND price. This indeed looks true based on a graph of BND with /10Y:

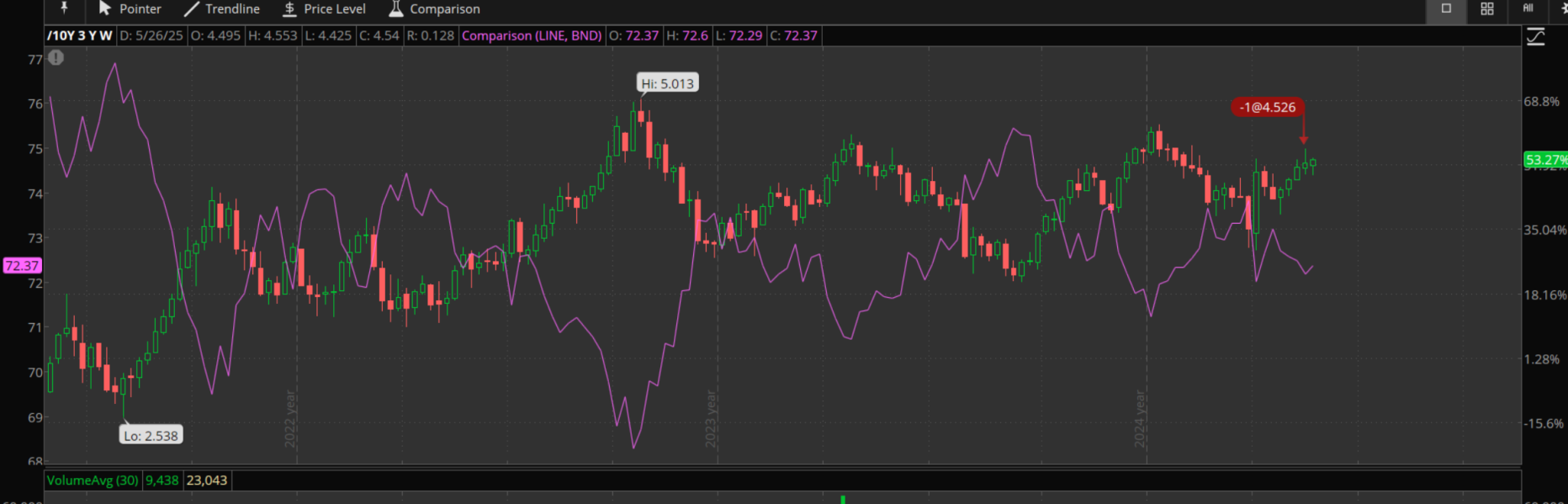
Buying BND might be equivalent to shorting (selling) /10Y futures. Shorting /10Y means betting that current rates come down, which means bonds at older rates will go up in value. From a portfolio standpoint, bonds are usually included to reduce volatility. They also give some income, so I'm not yet sure if the short futures position can be considered equivalent. It is something to test long term.

See Understanding Treasury Futures from the CME.

Cash loans with leverage

In many cases you will use the cash you received using leverage to buy further investments. However, this cash can be used for anything you want. The interest rates on these loans can beat standard bank loans. You can even opt to never pay the loan back, which is essentially the "buy, borrow, die" strategy. When you die, whoever inherits your equities will get their cost-basis reset to the value at inheritance, which means no capital gains if they sell.

Taking a cash loan from your stocks is essentially a leveraged trade. You have pulled money out while keeping your stocks, therefore you have increased your leverage. As an example, let's say I have $325k in stocks. Without any loan, my leverage ratio as defined above is:

\[\text{Leverage Ratio} = \frac{\text{Notional Exposure}}{\text{Portfolio Equity}} = 1\]

Both notional exposure and portfolio equity is equal, so my leverage ratio is 1. Let's say I now pull out $100k in cash, taking a margin loan. My leverage ratio becomes:

\[\text{Leverage Ratio} = \frac{325000}{325000 - 100000} = 1.44\]

With different leveraging strategies I can achieve the same leverage in multiple ways. In this case I've just used a margin loan.

Let's say instead I start with $325k in cash, and no equities. My leverage ratio is 1. I buy 1 /ES S&P 500 future, which has about $325k in notional value and requires about $25k cash set aside (margin requirement). As it stands my leverage ratio is:

\[\text{Leverage Ratio} = \frac{325000}{325000 - 25000} = 1.08\]

There is now $300k leftover in cash. If I start withdrawing cash, the leverage goes up, and I can easily match the 1.44 in the first example. Suppose I withdraw $75k in cash:

\[\text{Leverage Ratio} = \frac{325000}{325000 - 25000 - 75000} = 1.44\]

I've essentially done the same thing as a margin loan, albeit for a smaller cash loan ($75k vs $100k). With the margin loan, there is the daily interest cost. With the futures "loan", the interest is baked in because the futures quote for a later date will be higher than the current index quote.

How can we compare the interest rates? For the margin loan it is simple and is what the brokerage gives us, say 6%. The cost of 1 year borrowing $100k is $6k.

For the futures trade, let's look at an example with current quotes. Say the current S&P index is 6466. A futures contract of length 117 days is 6541. So the upfront cost is 6541-6466 = 75. That is 75/117 per day or ((75/117)*365) per year: $234.

That means for our loan of $75k, the interest rate is (234/75000) or about 0.3%. That is much lower than 6%. I'm likely calculating this wrong and ignoring other costs, but hopefully the point comes across.

This example is mainly to show that these loan instruments are interchangeable and it all comes down to how you achieve leverage and its associated cost.